Matematicas de Carlos

Una ecuación matricial es una ecuación donde la incógnita es una matriz.Para resolver una ecuación matricial se transforma la ecuación inicial en otra equivalente usando las propiedades de las matrices. Es muy importante tener en cuenta que las matrices no son conmutativas, por ello, si se quiere multiplicar una ecuación por determinada matriz hay que hacerlo en ambos términos de la igualdad por el mismo sitio.Supongamos que tenemos la ecuación matricial A·X=B-C, esta ecuación tendrá solución si A es invertible. Multiplicamos a la izquierda por A-1 quedando A-1A·X=A-1(B-C) de ahí se deduce que X=A-1(B-C). Veamoslo con matrices
Sean las matrices Resuelve la ecuación A·X=B-CPor el razonamiento anterior X=A-1(B-C)Calculamos la inversa de A

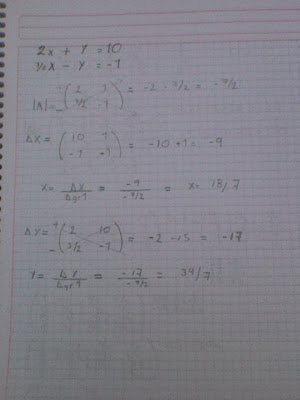
Regla de Cramer
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
La regla de Cramer es un teorema en álgebra lineal, que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752), quien publicó la regla en su Introduction à l'analyse des lignes courbes algébriques de 1750, aunque Colin Maclaurin también publicó el método en su Treatise of Geometry de 1748 (y probablemente sabía del método desde 1729).[1]
La regla de Cramer es de importancia teórica porque da una expresión explícita para la solución del sistema.
Computacionalmente, es ineficiente para grandes matrices y por ello no es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para las matrices pequeñas, particularmente cuando son usadas operaciones SIMD.
Si es un sistema de ecuaciones. A es la matriz de coeficientes del sistema, es el vector columna de las incógnitas y es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz A ha de ser no nulo.